Opgave 1: Dagens wetware-opgave

Hvad er $\,\displaystyle{\sin\left(3\frac{\pi}{2}\right)}\,$?
Opgave 2: Fra vinkelmål til radiantal og omvendt
Angiv de radiantal der svarer til vinkelmålene $30, 60, 120, 135$ og $300$ grader.
Tegn enhedscirklen i et $(x,y)$-koordinatsystem med centrum i Origo. Afsæt punkter på enhedscirklen svarende til buelængderne
Hvilke vinkelmål i grader svarer de til?
Opgave 3: Cosinus og Sinus
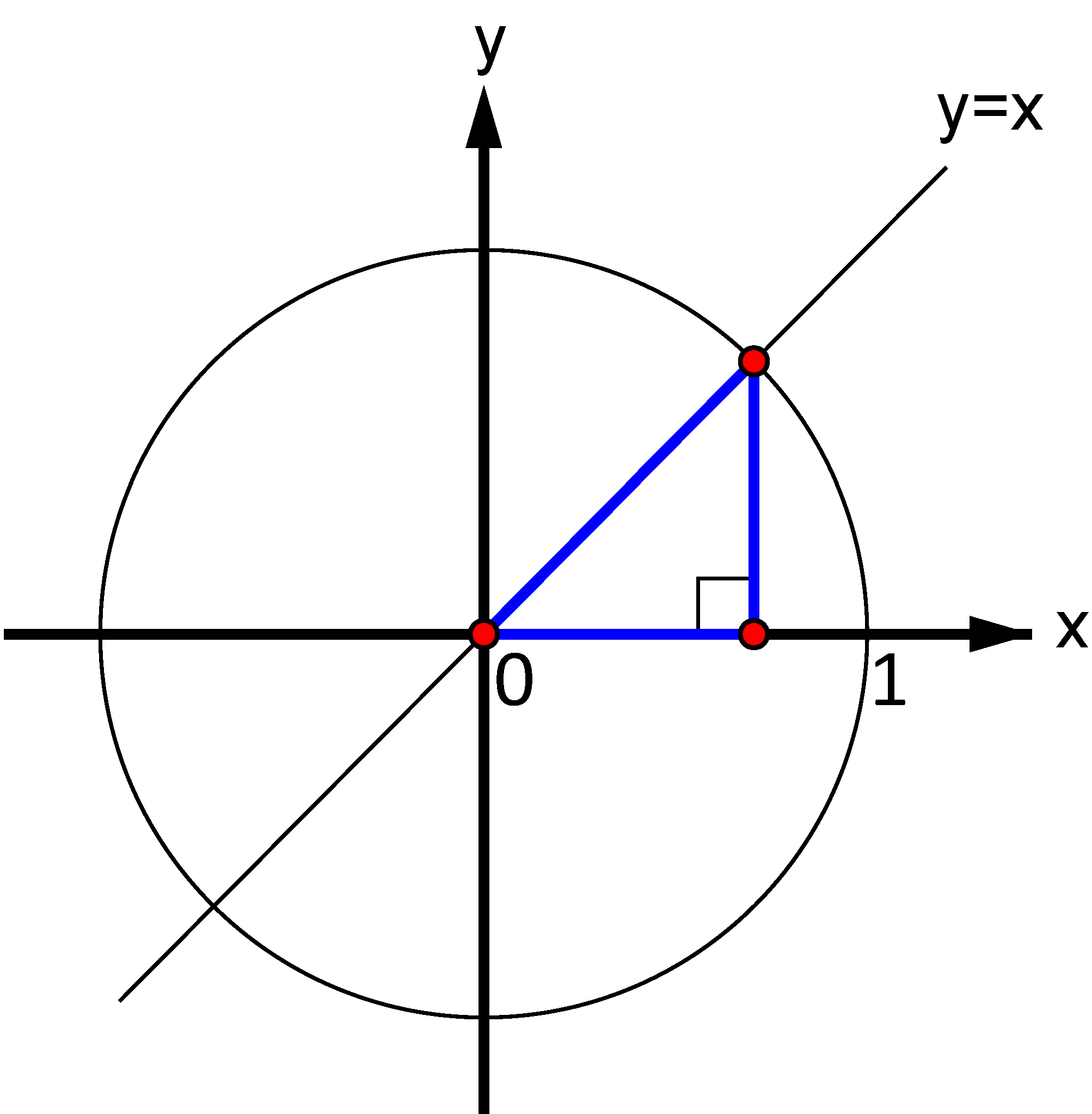
Benyt figuren (den blå trekant) til geometrisk bestemmelse af de eksakte værdier for $\,\displaystyle{\cos\left(\frac{\pi}{4}\right)}\,$ og $\,\displaystyle{\sin\left(\frac{\pi}{4}\right)}\,.$
Bestem ved hjælp af symmetribetragtninger tallene
Det oplyses at $\,\displaystyle{\cos\left(\frac{\pi}{6}\right)}=\frac{\sqrt 3}{2}\,$ og $\,\displaystyle{\sin\left(\frac{\pi}{6}\right)}=\frac{1}{2}\,.$ Indtegn punktet
på en enhedscirkel og find ved hjælp af symmetribetragtninger tallene
For givne tal $\,A,\,b,\,C\,$ og $d$ er graferne for funktionerne
plottet for $\,x\in \left[\,-\pi\,,\,\pi\,\right]\,$.
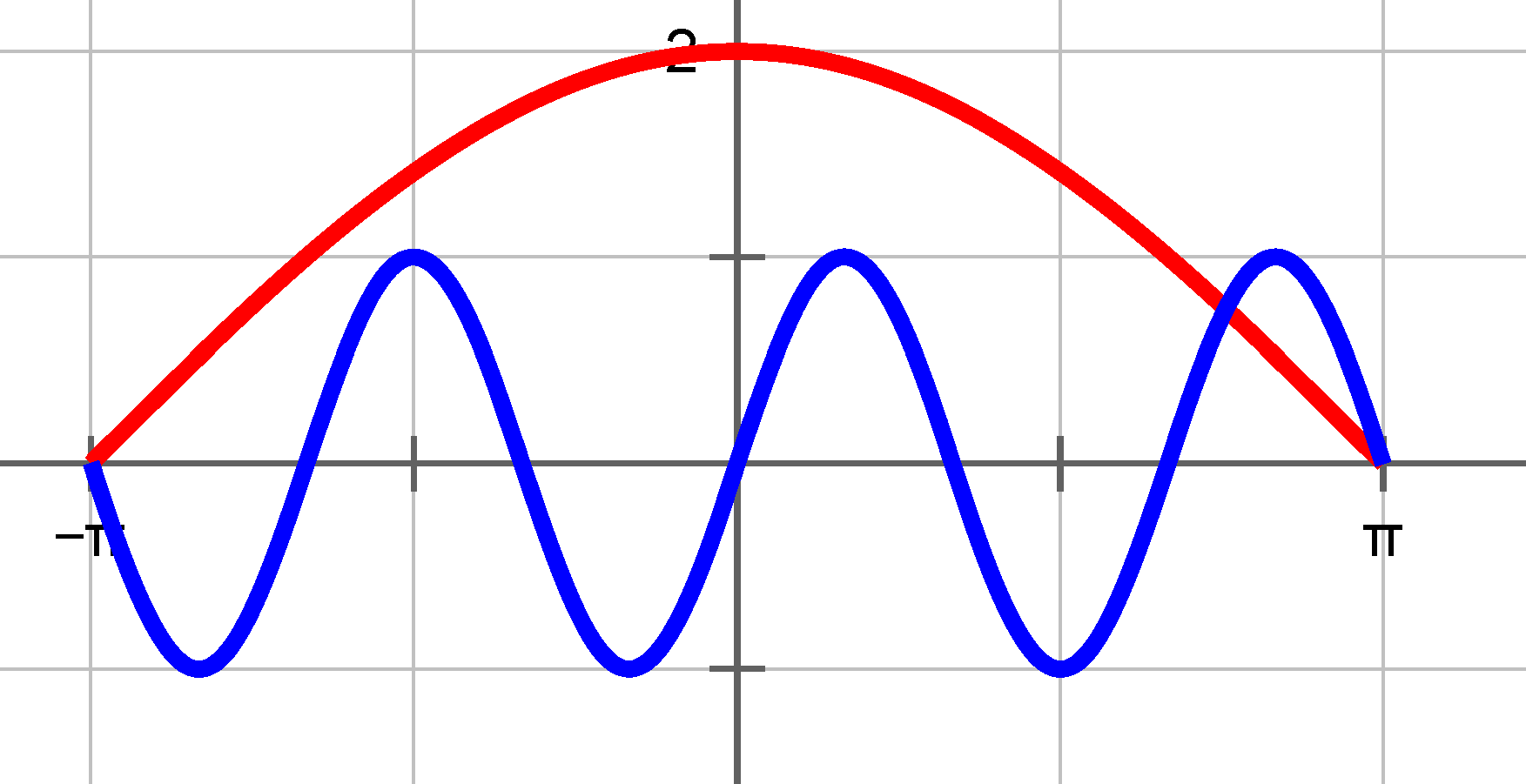
Bestem tallene $\,A,\,b,\,C\,$ og $d\,.$
Opgave 4: Polære koordinater
Givet tallene $z_0=1+i\sqrt{3}\,$, $z_1=-1+i\sqrt{3}\,$, $z_2=-1-i\sqrt{3}\,$ og $z_3=1-i\sqrt{3}\,$.
- Find den cirkel med centrum i $0\,$, hvorpå de fire tal ligger.
- Bestem $\,\arg(z_0)\,$, og angiv derefter hovedargumentet for $\,z_1\,,\,z_2\,$ og $\,z_3\,$. Hvad er de polære koordinater for alle fire tal? $ $
En studerende skal finde de polære koordinater for tallet $\,2-2i\,\,$. Han vælger at bruger lommeregneren. Ved at indtaste
får han absolutværdien til $\,2\sqrt{2}\,.$ Og ved at indtaste
får han argumentet til $\,\displaystyle{\frac {\pi}4}\,.$
Tjek udregningerne. Hvori består den studerendes fejl?
Find absolutværdi og hovedargument for følgende komplekse tal:
-
$-2+2i$.
-
$\displaystyle{-\frac{1}{6}+\frac{i}{2\sqrt{3}}}\,$.
Tre komplekse tal er givet ved deres polære koordinater således:
Find tallenes rektangulære form.
Opgave 5: Komplekse tals eksponentielle form
Skriv følgende komplekse tal på rektangulær form:
-
$\e^{i\frac{\pi}{2}}$
-
$3\e^{1+\pi i}$
Givet tallene $z_0=1+i\sqrt{3}\,$, $z_1=-\sqrt{3}+i\,$, $z_2=-1-i\sqrt{3}\,\,$ og $\,z_3=\sqrt{3}-i\,$.
-
Angiv de fire tal på eksponentiel form.
-
Vis at der findes en ligning af formen
(en binom ligning) hvori alle fire tal er en løsning.
Opgave 6: Den komplekse eksponentialfunktion
Givet $w=1-i\,$.
-
Bestem $|\,w\,|$ og $\arg(w)\,$.
-
Bestem $|\,\e^w\,|$ og $\arg(\e^w)\,$.
- Givet tallene $\,w_1=1\,,\,w_2=\e\,,\,w_3=i\,$ og $\,w_4=2i\,$. Bestem samtlige løsninger for ligningerne
hvor $\,n=1\,.\,.\,4\,$.
- Bestem samtlige løsninger for ligningen
Vis at $\,\e^z\neq0\,$ for alle $\,z\in\mathbb C\,$.
Opgave 7: Geometrisk addition og multiplikation
Hvis du ikke allerede har GeoGebra installeret på din computer, så gør det nu. Se linket til GeoGebra på Dagsordnen for i dag.
Åbn GeoGebra-arket komplekseTal (måske nemmest at højreklikke + gem som). Der er i arket givet fire komplekse tal $\,z_1,\,z_2,\,z_3\,$ og $\,z_4\,.$ Konstruér de følgende komplekse tal
Tegn derefter med vektorværkøjet (som ligger i linje-kassen) de fundne komplekse tals stedvektorer. Giv dem evt. en anden farve. Træk til sidst de fem gule labels hen til de tilsvarende tal. NB: Du vælger i denne opgave selv dit ambitionsniveau (eller gå skridtvis frem fra nemmeste til sværeste): Mild: Højreklik på arket og aktivér Gitter. Vælg Lås til gitter i Indstillinger $\rightarrow$ Fang punkt. Find ved hjælp af geometriske betragtninger de ønskede tal og afsæt dem med punkt-værktøjet.\bs Medium: Konstruér de ønskede tal med særlige GeoGebra konstruktionsværktøjer, f.eks. Parallelforskyd med vektor og Spejl i punkt. Hot: Find tallene vha. af ren passer og lineal-konstruktion. Passeren finder du i cirkel-kassen. Lineal-konstuktion udføres med relevante værktøjer i linje-kassen.
Opgave 8: Dobbelte vinkler (advanced)
Her er de såkaldte formler for dobbelte vinkler:
Brug den sidste (sammen med idiotreglen) til at bestemme $\cos\left(\frac{\pi}{8}\right)\,$ og $\sin\left(\frac{\pi}{12}\right)\,.$
Brug det første resultat i A) at finde $\sin\left(\frac{\pi}{8}\right)\,,\cos\left(\frac{3\pi}{8}\right)\,$ og $\,\sin\left(\frac{3}{8}\pi\right)\,$.
Brug tilsvarende det andet resultat i A) til at finde cosinus og sinus til interessante vinkler af form
